The Stable Marriage Problem and Modern Dating
— Dating, Game Theory, Programming — 7 min read
This post is a follow-up to the intro post about The Stable Marriage Problem. Check out the previous post to understand the problem/solution because this post examines its implications, particularly in the modern dating world.
Modern Times
A fascinating consequence of the internet is how much closer it has brought the problem of finding your soulmate, as well as how much closer the assumptions in the original Stable Marriage Problem (SMP) are true in reality. The original paper from 1962 has assumptions that neither worked then nor now, but it started the discussion on how to best pair people for marriage and any entities for any purpose in general.
The original SMP assumes that everybody knows everybody so that each person can rank everyone in the opposite gender. This was a clearly unrealistic assumption back in 1962, however, nothing has been a more unifying resource in the history of humanity than the internet.
While the SMP may have been an interesting experiment to replicate in a small closed off town 25 years ago, people are finding other people at a much greater rate and from a larger and more diverse group, allowing the SMP to simulate real life more accurately.
The table below shows the top three ways people have met their partner by decade in the past 50 years:
| Decade / Rank | 1 | 2 | 3 |
|---|---|---|---|
| 1960’s | Through Friend (19%) | Through Family (13%) | Primary / Secondary School (12%) |
| 1970’s | Through Friend (21%) | Through Family (13%) | Bar / Restaurant (10%) |
| 1980’s | Through Friend (18%) | Through Coworker (16%) | Bar / Restaurant (14%) |
| 1990’s | Through Friend (18%) | Through Coworker (15%) | Bar / Restaurant (12%) |
| 2000’s | Through Friend (19%) | Bar / Restaurant (11%) | Through Coworker (10%) |
| 2010’s | Met Online (19%) | Through Friend (17%) | Bar / Restaurant (15%) |
The 2010’s showed a monumental rise in online dating, and the number of people who have met their significant other online is only going to continue to grow. Online dating is interesting in particular because it provides us with a breadth of information on dating patterns in the modern age.
I wanted to see how the SMP actually worked when run through some simulations, and how well it actually models real life.
In order to benchmark some variants of the SMP that model real life more accurately, let's start off by simulating the classic problem scenario proposed over 50 years ago.
Simulations
Classic
I created a Python implementation of the classic SMP solution in order to calculate some initial results on what a 'perfect' world would be like.
The main assumption in the classic SMP scenario is that everybody knows each other and that people's preference towards the opposite group is randomly and uniformly distributed. This basically means that everybody has an equal chance to be liked by someone of the opposite gender.
The standard algorithm was run with different population levels - the number of iterations to find a stable matching as well as the average preference rank each person matched with was recorded.
The latter point is shown in the second graph and is portrayed as the difference between the rank of what every girl got, minus the rank of what every guy got (notice the title indicates an advantage for men, this is because in pretty much all scenarios the man came out higher in the matching, a.k.a the 'reacher')
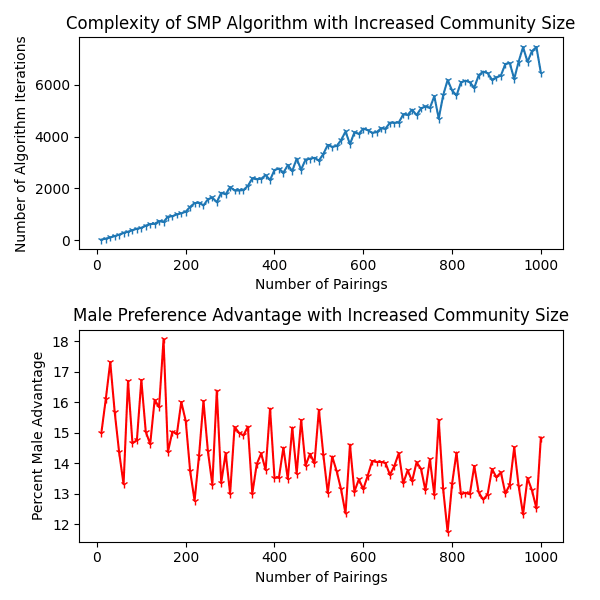
From the simulations we can observe two things:
The first graph demonstrates the
O(n²)complexity of the algorithm. We can see that as the community grows larger, even by a small amount, the amount of iterations it takes to solve the matching problem grows exponentially.- It shows how the difficulty of finding a stable matching between two people grows at a disproportionate rate when population of the community increases.
The second graph shows the difference in preference ranks for each group of people. It is calculated by examining each matching and seeing where the woman lies on the man's preference rank and where the man lies on the woman's preference rank.
Since the only difference between the two groups is which group 'proposes' first, we see as an outcome that men have an advantage in this scenario in that, compared to women, they end up with a partner higher on their preference list.
The advantage starts off high, and seems to converge at around 13-14% advantage for men
Preference Manipulated by Dating Pattern
There are some pretty large assumptions being thrown around in the classic SMP scenario.
In my opinion, the biggest assumption made is that preference sets are randomly assigned and uniformly distributed. This means that everyone's preference is not correlated with one another's, and that for large enough populations everyone's attractivness is roughly the same (based on how the opposite gender ranks).
I don't know about you, but I certainly don't have an online following of girls gushing over me like Timothée Chalamet does.
As mentioned before, one of the interesting ramifications of the rise in online dating is the amount of data we can aggregate from it.
OkCupid periodically releases dating information in their blog, and some time ago they released some interesting numbers in how men perceive attractiveness of the opposite sex versus women. The following charts outline the discrepancy:
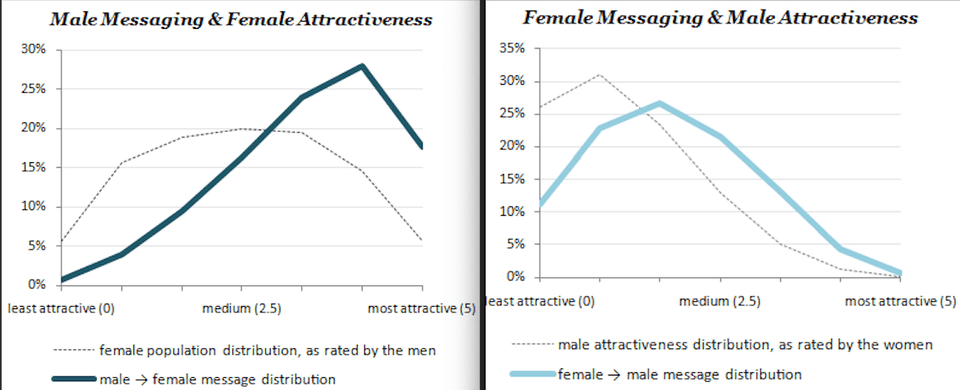
From the data (specifically the dotted lines) we can see two things:
Men's ranking of women pretty closely resembles a normal distribution. This is easy to conceptualize as essentially half of women in mens eyes are above average and half are below.
Women's ranking of men is more closely related to the Pareto distribution, also known as the 80-20 distribution. With respect to this problem, it means that if we could quantify attractiveness for every guy, the top 20% of men hold 80% of cumulative attractiveness in the eyes of women. In an unrelated note, Bernie seems a lot more appealing right about now.
So how do we change our problem?
We can tweak our original code so that each gender's preference rankings are more aligned with their respective distribution of opposite sex attractiveness.
Here is the updated code. Take a look in particular about the shuffling code for preference lists. The new shuffling code applies the normal distribution for guys and pareto distribution for girls.
I ran the same simulations again with the updated code and it produced the following results:
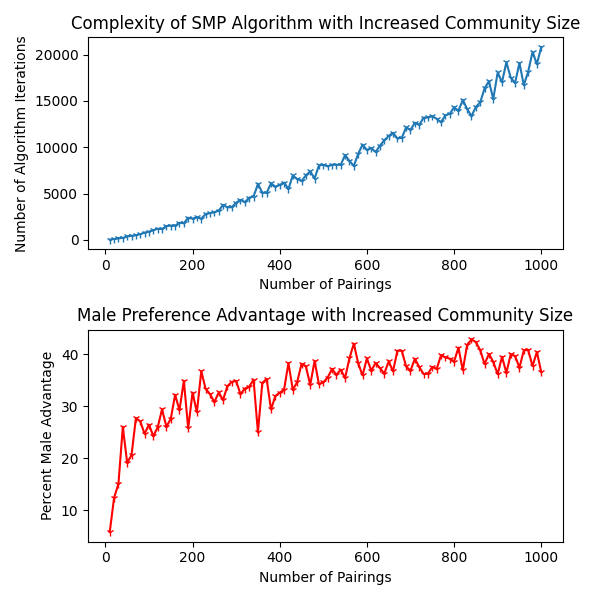
This is the same type of data analyzed from the previous simulation, but with much different results:
The first graph shows a similar
O(n²)complexity of the algorithm, but the constant value for the graph's equation is much higherThe standard SMP for 1000 pairings took around 7,000 iterations to complete - with the new simulations, the SMP algorithm runs in about 21,000 iterations, or 3 times as much
This makes sense in terms of the distributions. Since more women now have the same few men in the top 20% of their preference lists, the number of conflicts increases when running the algorithm and causes a lot more men to be dumped and subsequently resume their search for a better soulmate
The second graph is particularly interesting and shows a marked increase in the 'advantage' men have simply for being the proposers
The increase here stabilizes at around 38-39% and is again around 3 times larger than the advantage men had in the classic SMP scenario
This increase also makes sense because of the discrepancies in preferences between men and women. If the average man was paired with the average woman, the OkCupid data shows that the man would see the woman as average in attractiveness while the woman would see the man as below average attractiveness
What Did We Learn From This?
There's obviously many gross inaccuaries when trying to reasonably model the dating world, but the SMP offers an initial glimpse as to why dating is so difficult and why certain tropes exist.
Why it's always better to be the initiator
A clear callout from the analysis is that men end up having the advantage when everyone is paired. There's two main reason for this:
1) Societal Expectations:
Men are traditionally assumed to be the first group to make a move and it is why the men in the code simulations make the first move. Because men make the first move, the algorithm benefits men as it works in a greedy behavior to get them the best possible partner.
With respect to the problem, any gender can theoretically be the one to make the first move and reap the benefits demonstrated by the SMP simulations.
 ⠀From WikiHow, I can't really draw this well
⠀From WikiHow, I can't really draw this well
2) Preferences of Men vs Women:
The discrepancy in preferences for the opposite sex between men and women is what caused the stable pairing advantage for men to jump from 13% to 39%. While all other things are held constant, it was the preferences that caused this jump because it all ends up relating to how people perceive attractiveness.
The OkCupid data shows that women have higher standards for men than men have for women, and this is the main driver for why there is a larger male advantage when the SMP algorithm incorporated the gender attractiveness distributions.
I am in no way concluding that women are unhappier with men in their relationships - there are a million other factors including personality, status and chemistry that affect how each person in the relationship views each other.
However, it does lead us to how the outside world perceives the relationships...
Settlers and Reachers
The show How I Met Your Mother was a staple TV show during my coming of age years, and it surprisingly had many apt theories surrounding modern dating.
One of the most notable ones was the concept of Settlers and Reachers - as said in the show:
Every good relationship has a reacher and a settler. One person reaches for someone out of their league, while the other one settles for someone below theirs.
Based on everything we've learned thus far, we have seen that for the most part the men are the reachers and the women are the settlers.
Once again, this is just a generalization that only looks at pairings of men and women as a whole, and there are always examples that prove the opposite. But in my opinion, it does explain why in so many relationships that I see, my initial appearance based reaction is that the guy is punching above his weight class.
And there's plenty of media examples to back this up.
 ⠀⠀The guys really do be having a good personality though
⠀⠀The guys really do be having a good personality though
The observation is also noted by critics as the Movie and Television's attractiveness gap. And there's even a TV tropes article for it!
Modern Dating is harder than ever
Lastly, this point is about the complexity of the SMP algorithm and why it matters.
You can throw a rock towards any college and it would probably
hit a student in an overcrowded Computer Science class who would be ecstatic to tell you all about why an O(n²) algorithm is the worst thing since jorts.

The exponential nature of this algorithm shows that as a given community grows, it becomes exponentially harder to match people in a stable manner.
If you grew up in Tolono, Illinois, and all you've ever known were the proud people of Tolono, you'll probably find an easier time finding a partner than if you packed your bags and ran off to the Big Apple.
It is why it was much easier (in my opinion) to find a partner 30 years ago than it is today. Our commmunity has become increasingly global, and we're meeting people from all walks of life through all of our technological achievements.
Of course, this is all undeniably better for the advancement of the human race, however, it does make dating now just a little bit harder.
Did I write all of this to justify why I'm single?