Visiting the Stable Marriage Problem
— Game Theory, Economics — 4 min read
As much as I would’ve liked to write about how to save a dysfunctional marriage, this post is unfortunately not that - despite what the title may imply. What I really want to talk about is a mathematical (economists will claim it’s theirs) problem that I stumbled upon one night during my weekly Wikipedia binges.
The Stable Marriage Problem is an exercise of allocation theory, a field of study recently popularized by Alvin Roth and Lloyd S. Shapley by their Nobel Prize Winning Paper, The theory of stable allocations and the practice of market design. However, the actual problem has been proposed and solved for over 50 years now and has been used in many real world applications.
The stable marriage problem attempts to deterministically find pairings of people in a community such that both people in the relationship are content with their partner so that they can live happily ever after. And they say romance is dead 😉
Let’s Solve This Thing
The stable marriage problem is defined as follows:
1Find a stable matching between two equally sized sets of elements2where each element has a preference ranking of all the elements3in the opposite set.4
5A matching is stable if there are no unstable pairings.6
7An unstable pairing happens in the following example:8
9A and B from one set gets paired with 1 and 2 respectively from10the other set. However, B prefers 1 and A prefers 2.I’m not keen on movies containing a dorky nerd with glasses rambling on about something science-y while the protagonist responds with an “English Please!”, but a real-life example really does help understand the problem.
The name of the problem comes from the attempt to find pairings of men and women (I know this is 2020 but for the sake of the problem let’s assume all people are heterosexual) best suited for marriage. So suppose we have 3 men and 3 women that we’re trying to ship.

All 6 people have a preference ranking, from most to least desirable, of all the people in the opposite set.
Can we find 3 pairings such that all the pairings are not unstable? i.e., Other than the original 3 pairings, there’s no man/woman pair such that both people prefer each other over their current (original pairing) partner.
In 1962, David Gale and Lloyd Shapley proved that there exists an algorithm to find a stable matching for any given input. I’m not going to go into too much of the technical details, but the high-level process is as follows:
Step 0 - We start off with a community of N women and N men, each with their own preference rank of the opposite group
Step 1 - In the first iteration, every man proposes to their top pick
- Every woman reviews their received proposals (if any) and chooses their highest preferred person for a 'temporary engagement' (or, the dating phase)
- At this point, we may have some temporary engagements while the rest of the people are still unmatched
Step 2 - In the second iteration, each man with a rejected proposal then proposes to their second pick in their preference list, regardless if they’re available or not (a little suspect, but deal with it)
- Women can then break their tentative engagement if the next proposal is better, or they can keep it if not
Step N - We keep performing the steps in the second iteration where the men continue going down their preference list until all the people in the community are paired
Let’s see how this works in our example.
First Iteration
Men
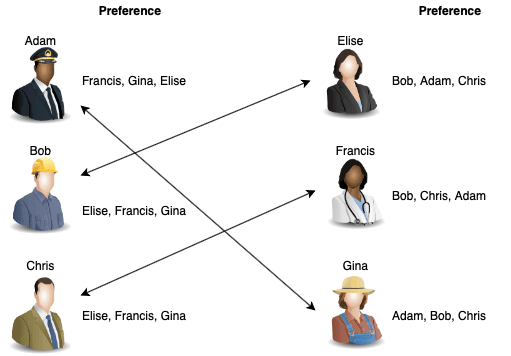
Adam proposes to Francis, Bob proposes to Elise, and Chris proposes to Elise
Women
Elise rejects Chris and accepts Bob’s proposal, Francis accepts Adam’s proposal, and Gina remains single :(
Outcome:
| Men / Women | Elise | Francis | Gina |
|---|---|---|---|
| Adam | MATCH | ||
| Bob | MATCH | ||
| Chris |
Second Iteration
Men
Chris proposes to Francis (who is already engaged)
Women
Francis accepts Chris’ proposal and leaves current partner Adam :(
Outcome:
| Men / Women | Elise | Francis | Gina |
|---|---|---|---|
| Adam | |||
| Bob | MATCH | ||
| Chris | MATCH |
Third Iteration
Men
Adam proposes to Gina
Women
Gina accepts Adam’s proposal
Outcome:
| Men / Women | Elise | Francis | Gina |
|---|---|---|---|
| Adam | MATCH | ||
| Bob | MATCH | ||
| Chris | MATCH |
Since all people are engaged, we have found a stable matching and everyone will become permanently engaged to their partner, as shown below:
The Gale-Shapley Algorithm is a neat little algorithm that runs in O(n²):
1algorithm stable_matching is2 Initialize all m ∈ M and w ∈ W to free3 while ∃ free man m who still has a woman w to propose to do4 w := first woman on m's list to whom m has not yet proposed5 if w is free then6 (m, w) become engaged7 else some pair (m', w) already exists8 if w prefers m to m' then9 m' becomes free10 (m, w) become engaged 11 else12 (m', w) remain engaged13 end if14 end if15 repeatMy own Python implementation of the algorithm can be found here
Although this algorithm is nice and dandy, and even has real-world applications, there are a few critical assumptions made here that most definitely do not apply to the modern dating world.
The glaring fault is that it assumes people have a strictly defined preference list on every person of the opposite gender and that they would leave their current partner immediately if it meant they had a shot at matching with someone even just one rank higher on their list.
The next blog post talks more about the conseuqences and limitations of the stable marriage problem and offers some variants that match closer to modern dating.
Real World Applications and Other Variants
To conclude this post, I wanted to briefly mention some of the real world examples and variants of the stable marriage problem.
Residency
The most well-known application of the Gale–Shapley algorithm is with the National Resident Matching Program.
Newly minted medical students create a preference list of residency/fellowship programs that they want to join. What most people don't know is that the same programs also create a preference list for the applicants!
Now that we have two sets of entities where each set contains a preference list of the opposite set (applicants to the programs and programs to applicants) we have all that we need to run a variant of the Gale-Shapley algorithm to find a stable matching.
The full paper is The Redesign of the Matching Market for American Physicians: Some Engineering Aspects of Economic Design
Stable Roommates
A very similar problem is the stable roommates problem. The only difference in this problem is that there is only one set of entities to choose from.
In the stable marriage problem, we have men and women in two different sets, but with the stable roommates problem we have
one singular set of people trying to find the best matching roommate given everyone's preferences. A similar O(n²) algorithm
exists which determines if there is a stable solution, and if so, outputs what it is.
What's interesting about this problem is that a stable solution is not guaranteed like it is with the stable marriage problem.
Therefore, theoretically, if people were as picky (adherence to preference list) about their roommates as they are with picking out a partner, then finding a roommate is actually a much harder thing to get right!
Closing Thoughts
The field of matching markets and entities is a relatively new concept in the economics world and it is continually growing. It offers a glimpse to solve a fundamental problem of economics, "how do we best allocate resources".
Pretty fundamental for an algorithm meant to simulate arranged marriages!
Check out the next post for a deeper analysis of the problem with respect to modern dating